Trong không gian với hệ tọa độ \(Oxyz,\) cho hai đường thẳng:
\( (d_1): \left\{\begin{aligned} &x=1+t \\ &y=2+t\\ &z=-2-t \end{aligned}\right. (t \in \mathbb R) \) và \( (d_2): \left\{\begin{aligned} &x=2+u \\ &y=1-u \\ &z=1 \end{aligned}\right. (u \in \mathbb R).\) Chứng minh rằng \((d_1)\) và \((d_2)\) chéo nhau. Viết phương trình của mặt cầu có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng \((d_1)\) và \((d_2).\)
Lời giải. Chứng minh \(\boldsymbol{(d_1)}\) và \(\boldsymbol{(d_2)}\) chéo nhau. Đường thẳng \((d_1)\) đi qua điểm \(M(1,\,2,\,-2)\) và có vector chỉ phương \(\overrightarrow{u_1}=(1,\,1,\,-1).\) Đường thẳng \((d_2)\) đi qua điểm \(N(2,\,1,\,1)\) và có vector chỉ phương \(\overrightarrow{u_2}=(1,\,-1,\,0).\) Ta tính được: \(\overrightarrow{MN}=(1,\,-1,\,3),\quad \left[\overrightarrow{u_2},\, \overrightarrow{u_1}\right] =(1,\, 1,\, 2).\) Từ đó suy ra \(\left[\overrightarrow{u_2},\, \overrightarrow{u_1}\right] \cdot \overrightarrow{MN}= 1\cdot 1 +1 \cdot (-1)+2\cdot 3=6 \ne 0.\) Kết quả này chứng tỏ \((d_1)\) và \((d_2)\) là hai đường thẳng chéo nhau.
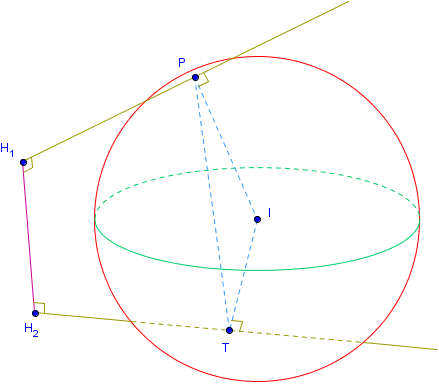
Viết phương trình mặt cầu \(\boldsymbol{(\mathcal S)}\) có bán kính nhỏ nhất tiếp xúc với cả \(\boldsymbol{(d_1)}\) và \(\boldsymbol{(d_2)}.\) Gọi \(I\) là tâm của \((\mathcal S);\) \(R\) là bán kính của \((\mathcal S);\) \(P,\,T\) lần lượt là các tiếp điểm của \((\mathcal S)\) và \((d_1),\, (d_2);\) và \(H_1H_2\) là đoạn vuông góc chung của \((d_1),\,(d_2).\) Sử dụng bất đẳng thức tam giác kết hợp với tính chất của đoạn vuông góc chung, ta thu được đánh giá: \(2R=IP+IT \ge PT \ge H_1H_2.\) Dấu bằng xảy ra khi và chỉ khi \(P \equiv H_1,\, T\equiv H_2\) và \(I\) là trung điểm của \(H_1H_2.\)
Từ đây, ta suy ra mặt cầu \((\mathcal S)\) thỏa mãn yêu cầu của đề bài có tâm \(I\) là trung điểm của \(H_1H_2\) với \(H_1H_2\) là đoạn vuông góc chung của \((d_1)\) và \((d_2).\)
Bây giờ, ta sẽ tìm tọa độ của \(H_1,\,H_2.\) Giả sử hai điểm này có tọa độ lần lượt là: \(H_1(1+t,\,2+t,\, -2-t),\quad H_2(2+u,\, 1-u,\, 1).\)
Khi đó, ta có \(\overrightarrow{H_1H_2}=(u-t+1,\, -u-t-1,\, 3+t).\)
Do \(H_1H_2 \perp (d_1)\) và \(H_1H_2 \perp (d_2)\) nên ta có
\(\left\{\begin{aligned} &\overrightarrow{H_1H_2} \cdot \overrightarrow{ u_1} =0 \\ &\overrightarrow{H_1H_2}\cdot \overrightarrow{u_2}=0\end{aligned} \right.\)
\( \Leftrightarrow \left\{\begin{aligned} &(u-t+1) \cdot 1 +(-u-t-1) \cdot 1 +(t+3)\cdot (-1)=0 \\ & (u-t+1)\cdot 1 +(-u-t-1)\cdot (-1) +(t+3)\cdot 0 =0 \end{aligned}\right.\)
\(\Leftrightarrow \left\{\begin{aligned} &t=-1\\ &u=-1
\end{aligned}\right.\)
Như thế, ta tìm được \(H_1(0,\,1,\,-1)\) và \(H_2(1,\,2,\,1).\) Từ đó, ta có \(I\left(\frac{1}{2},\, \frac{3}{2},\,0\right)\) và \(R=IH_1 =\frac{\sqrt{6}}{2}.\)
Vậy phương trình của mặt cầu \((\mathcal S)\) là: \(\left(x-\frac{1}{2}\right)^2+\left(y-\frac{3}{2}\right)^2+z^2 =\frac{3}{2}.\)